עיבוד מקבלי
- 157 שאלות
- 50 תגובות
- 0% הושלמו
- equalizer סטטיסטיקות
- share שתף
מנהלים:


Discuss, Learn and be Happy דיון בשאלות
help
brightness_4
brightness_7
format_textdirection_r_to_l
format_textdirection_l_to_r
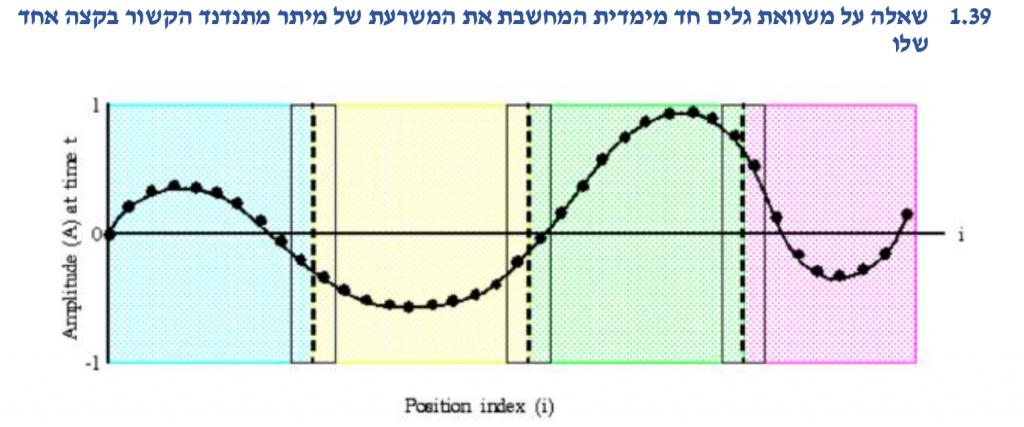
א. האם ניתן לכתוב תוכנית בשיטת SPMD שתדמה את הבעיה? ב. נבצע דיסקרטיזציה של המיתר ונשמור במערך את המשרעת שלו בנקודות אלה, ולאחר מכן נשלח למעבדים השונים את חלקי המערך המתאימים, האם מאותו שלב החישוב יהיה Embarrassignly Parallel עד סופו? ג. האם לצורך פתרון הבעיה נדרשות שכבות רפאים (ghost) בקו התפר שבין המעבדים כפי שמודגם בציור? ד. ככל שרוחב הפרוסות השייכות לכל מעבד יגדל כך ישתפר יחס זמני החישוב לתקשורת? ה. בבעיה הנתונה, האם שיפור ביחס זמן החישוב לזמן התקשורת גורר בהכרח קיצור זמן הריצה הכולל?
1
מיין לפי
א. האם התרשים מתאים לתיאור פקודת Broadcast (כל עיגול מייצג מעבד) ב . התרשים של סעיף א' יכול לתאר פקודת all reduce אם בכל עיגול יפעל אופרטור, כגון סכום, הפועל על הערך הנוכחי עם זה שמתקבל ממקור החץ אליו

1
| done | ||
מיין לפי
BLAS היא ספרייה מקבילית לאלגברה ליניארית
1
| done |
שימוש באסימון (token) יחיד יבטיח סיום ריצה מקבילית תקין בכל מימוש של pipeline
1
| done |
מיין לפי
מה שיש בתמונה

1
| done | ||
קודם כל tag בפקודות Send/Recv משמשות כדי להבדיל בין הודעות שונות שנשלחות, אם לא נגדיר tag אז recv יקבל כל send שישלח לאותו תהליך.
בקוד הנ"ל, נותנים מספר רנדומלי לtag לכן ה-recv לא יקבל את מה שמעבד 0 ישלח כי יהיה לו tag שונה מאשר ה-tag שבפקודת הsend של מעבד 0 (אנחנו רוצים שיהיה אותו tag) ולכן ההודעה לא תגיע ואז מפני שrecv היא פקודה חוסמת התוכנית תתקע.
דרך לתקן – לתת לשני הפקודות את אותו tag, למשל להגדיר: 3 = msgtag
מיין לפי
מוניטין: 60
קודם כל tag בפקודות Send/Recv משמשות כדי להבדיל בין הודעות שונות שנשלחות, אם לא נגדיר tag אז recv יקבל כל send שישלח לאותו תהליך. בקוד הנ"ל, נותנים מספר רנדומלי לtag לכן ה-recv לא יקבל את מה שמעבד 0 ישלח כי יהיה לו tag שונה מאשר ה-tag שבפקודת הsend של מעבד 0 (אנחנו רוצים שיהיה אותו tag) ולכן ההודעה לא תגיע ואז מפני שrecv היא פקודה חוסמת התוכנית תתקע. דרך לתקן – לתת לשני הפקודות את אותו tag, למשל להגדיר: 3 = msgtag






